みなさん二分探索アルゴリズムをご存知でしょうか?
wikipediaでは以下のように説明されています。
ソート済みのリストや配列に入ったデータ(同一の値はないものとする)に対する検索を行うにあたって、 中央の値を見て、検索したい値との大小関係を用いて、検索したい値が中央の値の右にあるか、左にあるかを判断して、片側には存在しないことを確かめながら検索していく。
https://ja.wikipedia.org/wiki/%E4%BA%8C%E5%88%86%E6%8E%A2%E7%B4%A2
二分探索アルゴリズムとは詰まるところ、「リストや配列の中の特定の値を高速で見つけることができるアルゴリズム」のことです。
目次
二分探索がどんなものかは理解できたところで、今度はそれを実装してみます。
ちなみに私は二分探索を実装できるようになるまで結構苦労しました…
まだ二分探索を実装したことがない方は以下の問題1を実装してみてください。
具体的な実装方法に関しては様々なサイトで解説されているので、そちらを参考にしてもいいかもしれません。
問題1
【問題1】
要素数nのソート済みの配列aの中に要素bが存在する場合はそのindex番号を出力し、要素が存在しない場合はNOと出力しなさい
1 <= n <= 10^18
aのなかに同じ値は存在しない
以下解答例
#include <bits/stdc++.h>
using namespace std;
vector<int> a = {1, 14, 32, 50, 51, 53, 243, 419, 750, 910};
// 配列aの中に要素bが存在する場合はそのindex番号を出力し、要素が存在しない場合はNOと出力しなさい
int main() {
// 標準入力
int b; cin >> b;
int start = 0;
int fin = a.size()-1;
int ans = -1;
while (start <= fin) {
int middle = (start+fin)/2;
if (a[middle] == b) {
ans = middle;
break;
}
if (n < a[middle]) {
fin = middle - 1;
} else {
start = middle + 1;
}
}
if (ans == -1) {
cout << "No" << endl;
} else {
cout << ans << endl;
}
}これが基本的な二分探索の実装になります。
解説
int start = 0;
int fin = a.size()-1;
int ans = -1;まずはこの部分で配列の最初と最後の位置を記録させておきます。

そこから真ん中の位置にあるindexの番号を求め、配列の真ん中の値を求めたい値を比較してその結果によってstartとfinの位置をずらしていきます。
32の場所を求めたい時を考えてみると以下のような動きになります。
実際に値を求める部分のコードは以下の部分です。
while (start <= fin) {
int middle = (start+fin)/2;
if (a[middle] == b) {
ans = middle;
break;
}
if (n < a[middle]) {
fin = middle - 1;
} else {
start = middle + 1;
}
}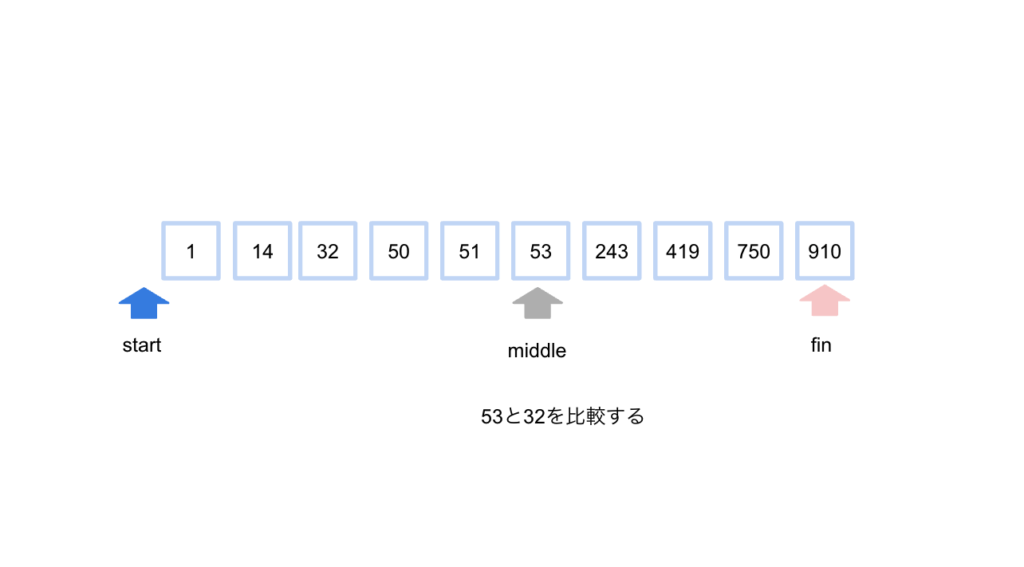
middleを求め、その値と求めたい値を比較していきます。
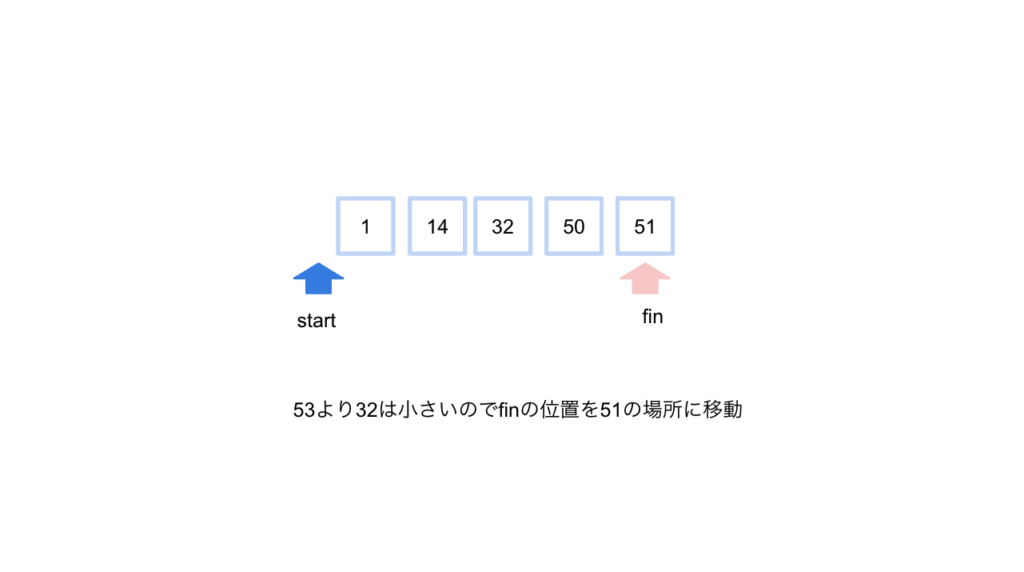
今回はmiddleより値が小さかったのでfinの位置を移動させます。
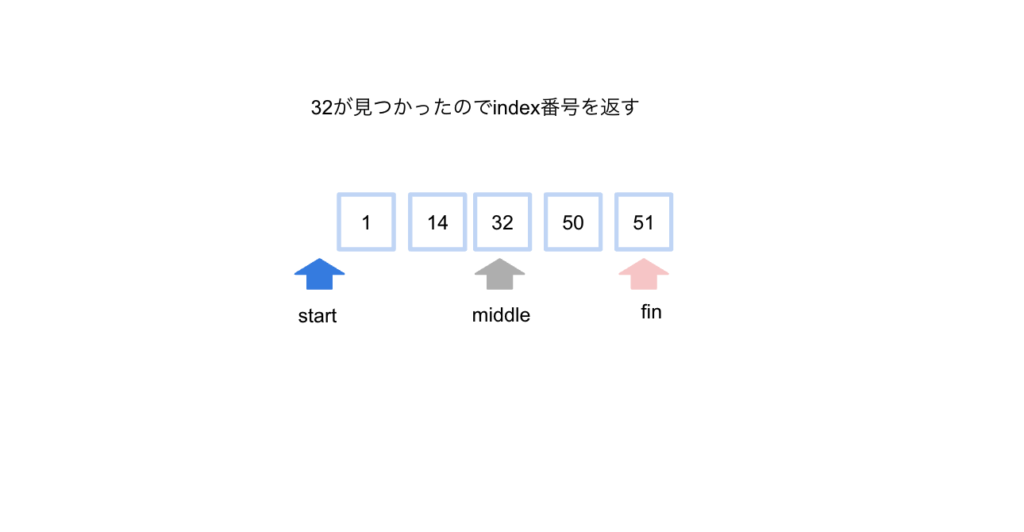
ここで32が見つかったので、そのindex番号を返します。
以上が二分探索の基本的な挙動です。
二分探索の実装方法と動き方のイメージは掴めたと思います。
ただ、この基本的な二分探索は既に言語のライブラリに存在することが多いです。
例えばrubyだとbsearchという組み込みライブラリが存在します。
ですので、実は問題1のような問題だと自前でコードを実装する必要はありません。
では、二分探索は自分で実装する必要がないのか?というとそうではありません。
以下のような問題を考えてください。
問題2
【問題2】
要素数nの配列aの中に要素が存在する場合はその要素が出現する最初のindex番号を出力し、要素が存在しない場合はNOと出力しなさい
1 <= n <= 10^18
問題1と問題2では大きく違うところがあります。
それは配列の中で同じ値の要素が存在することがあるということです。
例えば以下のような配列の場合で考えてみます。
a = {1, 1, 1, 2, 2, 50, 50, 50, 70, 70};ここで問題1での実装を見てみます。
while (start <= fin) {
int tmp = (start+fin)/2;
if (a[tmp] == b) {
ans = tmp;
break;
}
if (n < a[tmp]) {
fin = tmp - 1;
} else {
start = tmp + 1;
}
}上記のような実装だとマッチした最初のindex番号を返してしまいます。
つまり、配列aに含まれる1の最初のindex番号を考えた時、返される番号が配列の要素数によって異なってしまうのです。
最初の1のindex番号かもしれないし、2番目や3番目のindex番号が返される可能性がありこれでは正確な値を返すことができません。
このときに使うのが
「めぐる式二分探索」
です。
このめぐる式二分探索を用いることで、データ群の中で値を満たすゾーンと満たさないゾーンの境界を求めることができるようになります。
イメージとして配列aの中から値50を満たすゾーンと満たさないゾーンの境界を求めると以下のようになります。
a = {1, 1, 1, 2, 2, 50, 50, 50, 70, 70};解答例
問題2の解答例は「めぐる式二分探索」を用いることで以下のように実装することができます。
#include <bits/stdc++.h>
using namespace std;
vector<int> a = {1, 1, 1, 2, 2, 50, 50, 50, 70, 70};
// 配列aの中に要素が存在する場合はその要素が出現する最初のindex番号を出力し、要素が存在しない場合はNOと出力しなさい
bool isOK(int index, int key) {
if (a[index] >= key) return true;
else return false;
}
int main() {
// 標準入力
int n; cin >> n;
int left = -1;
int right = a.size();
if (a[0] > n || a[a.size()-1] < n) {
cout << "NO" << endl;
} else {
while (right - left > 1) {
int tmp = left + (right - left) / 2;
if (isOK(tmp, n)){
right = tmp;
} else {
left = tmp;
}
}
cout << right << endl;
}
}
解説
めぐる式探索の詳しい解説は以下を読むとわかりやすいです。
上記の記事の繰り返しになる部分もありますが、簡単に実装の解説をします。
2の最初のインデックス番号を調べる場合を考えます。
まずはrightとleft、中間値tmpの値を決めます。
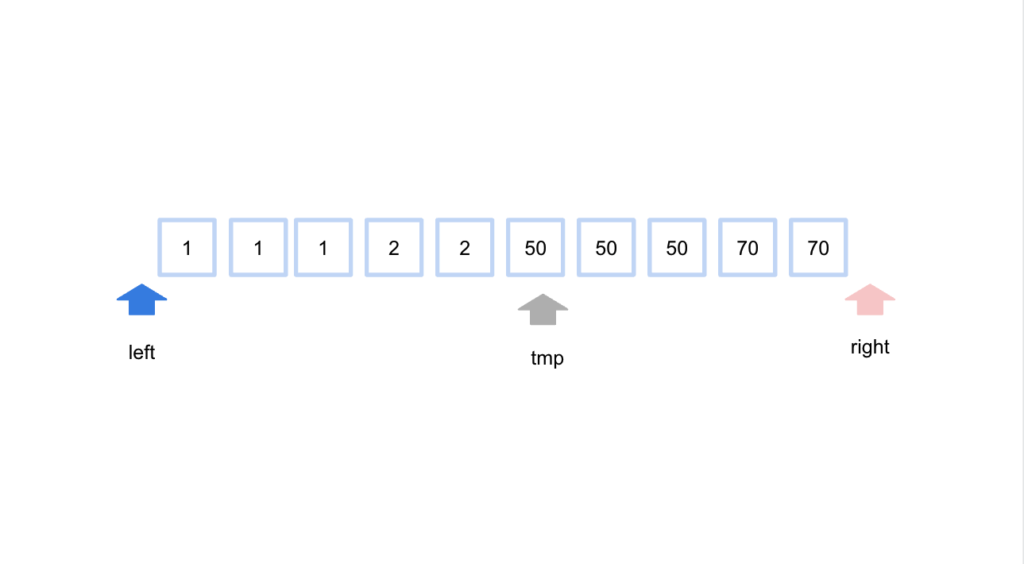
そしてisOKメソッドの引数に中間値と調べるべき値を渡して判定します。
今回は2と50を比較しているのでrightの位置が移動します。
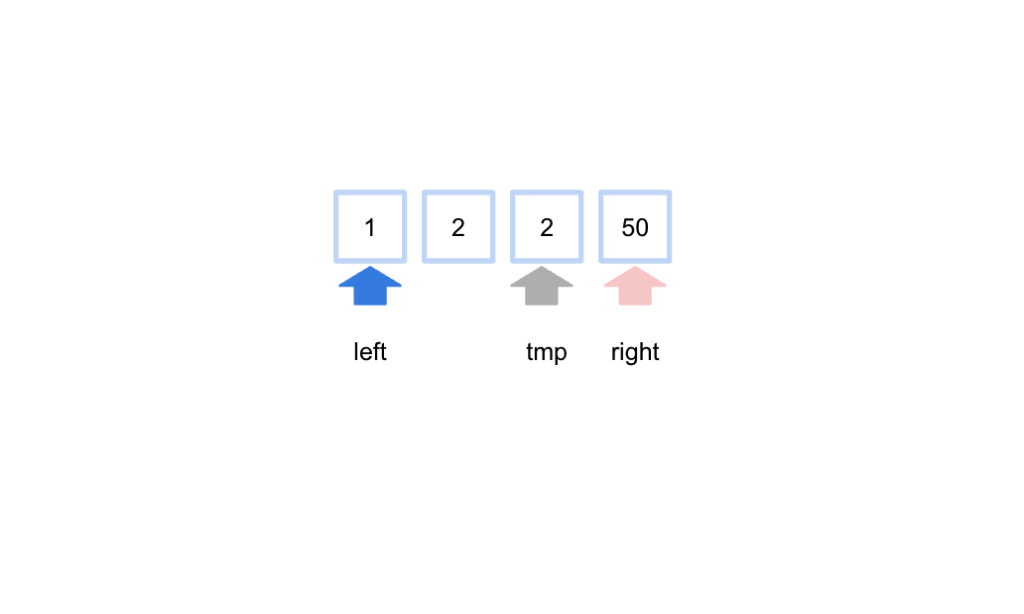
これを繰り返し、2が最初に出てくるインデックス番号を求めます。
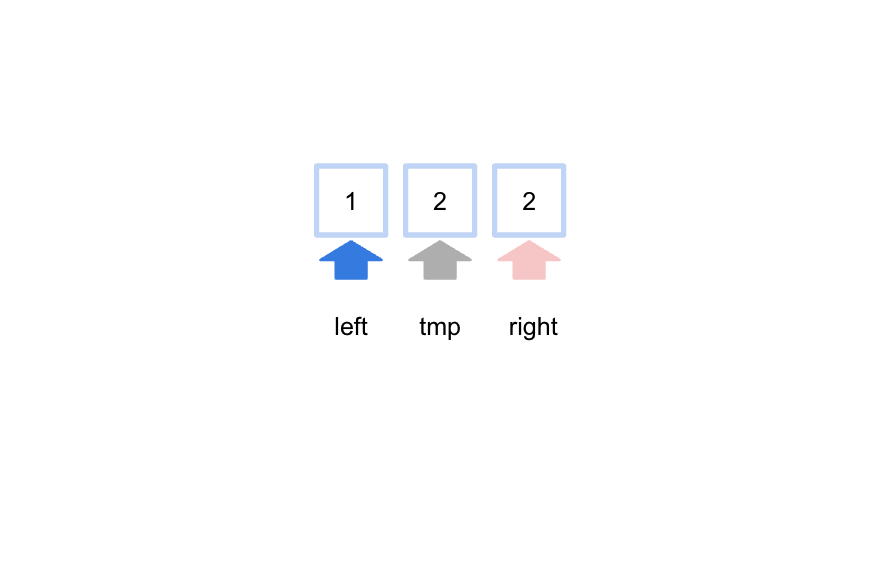
while (right - left > 1) {上記loopの条件からrightとleftが隣同士になるまでloopは終わらないのでもう一度loopの中に入ります。

ここで2が最初に出てくるrightの値を出力することで2が最初に出てくるインデックス番号を出力します。
ここでは二分探索とめぐる式二分探索についてまとめました。
ここで私が伝えたいのは、二分探索は値を見つけるためのアルゴリズムではなく、値と値の境界線を求めるためのアルゴリズムということです。
みなさんも実際に値と値の境界を求める必要が出てきた場合には二分探索を用いて高速に処理できないか考えてみてください。
他にもアルゴリズムについてまとめている記事があるのでそちらもご覧ください
 ハノイの塔アルゴリズムをわかりやすく解説する
ハノイの塔アルゴリズムをわかりやすく解説する
 takatoku-room
takatoku-room 
