ハノイの塔という問題をご存知でしょうか?
ハノイの塔アルゴリズムを理解できなくて苦労したので、記録のためにも私がハノイの塔アルゴリズムをどのように理解したのか書いていきたいと思います。
目次
ハノイの塔問題の説明
ハノイの塔はパズルの一種です。
3本の杭があり、左端の杭に複数の中央に穴の開いた大きさの異なる円盤があった時に、ある一定のルールに従って異なる杭にその円盤を全て移動させるという問題です。
「ある一定のルール」これがハノイの塔アルゴリズムを理解する上で大切になってきます。
そのルールとは以下の2つです。
- 円盤を一回に一枚ずつどれかの杭に移動させることができる
- 小さな円盤の上に大きな円盤を乗せることはできない
試しに3枚の円盤ではどのように動かしているのか図で見ていきます。
最初は左の杭aに円盤があります。
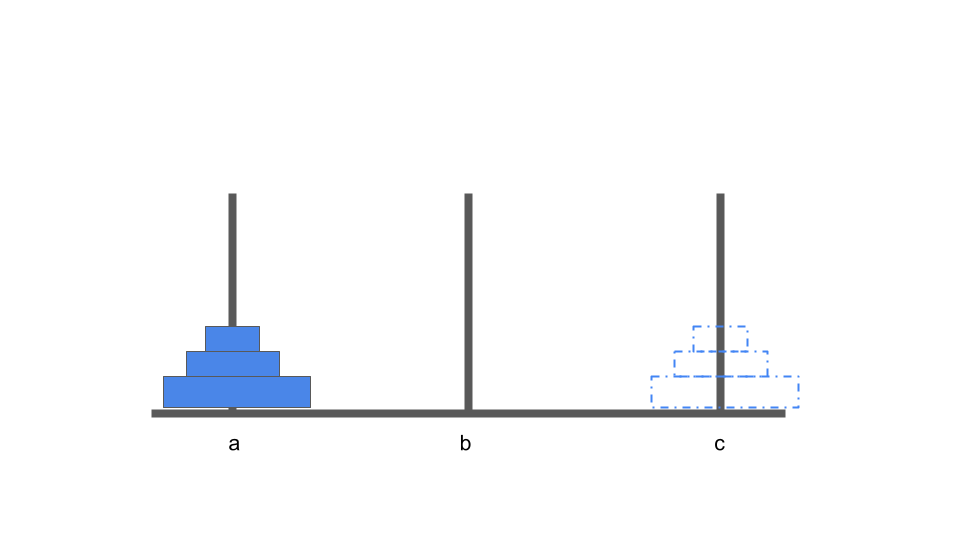
この円盤をを杭cに移動することを考えます。
ルールに沿って円盤を動かしていくと以下のようになります。
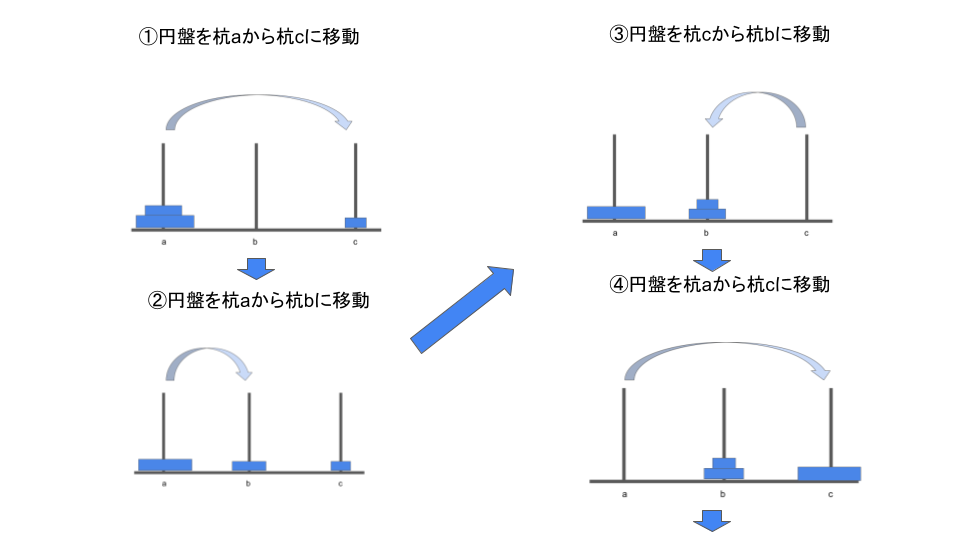
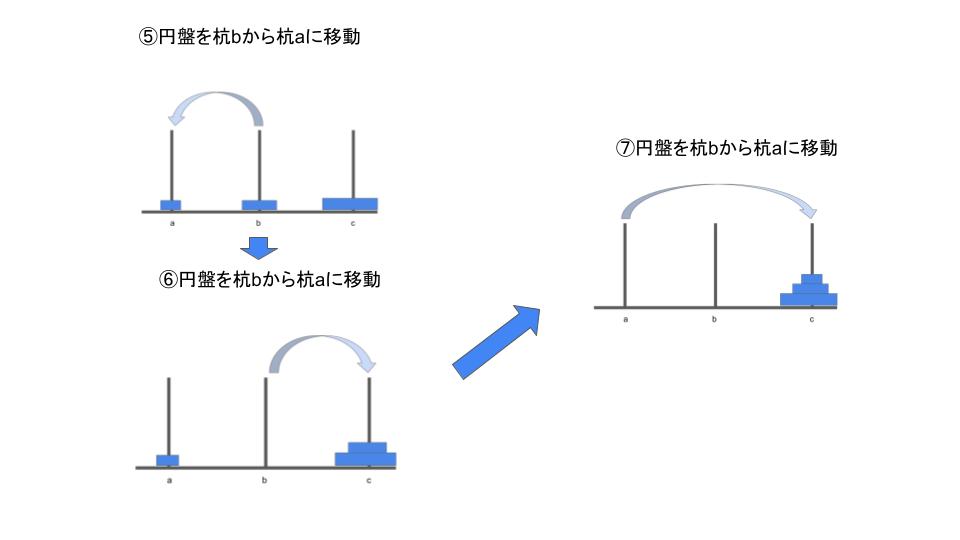
この移動をコードで再現します。
ハノイの塔アルゴリズムをわかりやすく解説
この問題でやっていることは全て、杭から杭に円盤を移動させているだけです。
ですので、再起関数を使えばいけそうな気がします。
再起関数についての説明はは以下の記事をで説明しているので参考にしてください。
 コードを見ながら理解する「入れ子構造」と「再起関数」
コードを見ながら理解する「入れ子構造」と「再起関数」
このアルゴリズムを考える上で、重要のなのは一つ一つの移動の法則に囚われすぎないことです。
ここでいう「一つ一つの法則」とは
「まずは1番上の円盤を杭cに移動して、その後2番目の円盤を杭bに移動する、その後は最初の円盤が杭cにあるから…」
と実際の手順全てのことを表しています。
円盤を動かす手順を見て一つ一つの移動の法則を見つけようとしてはいけません、円盤移動の行程全体をみてどういう処理を繰り返せばいいのかということにだけに意識を向けます。
それでは、実際の手順からハノイの塔アルゴリズムの「捉え方」を解説していきます。
まずルールに則って考えると、一番下の円盤を移動対象の杭cに移動させることを考えなければいけません。一番下の円盤を杭cに移動した後は、その円盤を移動させる必要はなく、残りの円盤をどう積み上げていくのかを考える必要があります。
ということは、杭cに移動し終わった円盤は無視していいということになります。
それでは③の状態と⑤の状態に注目してください。
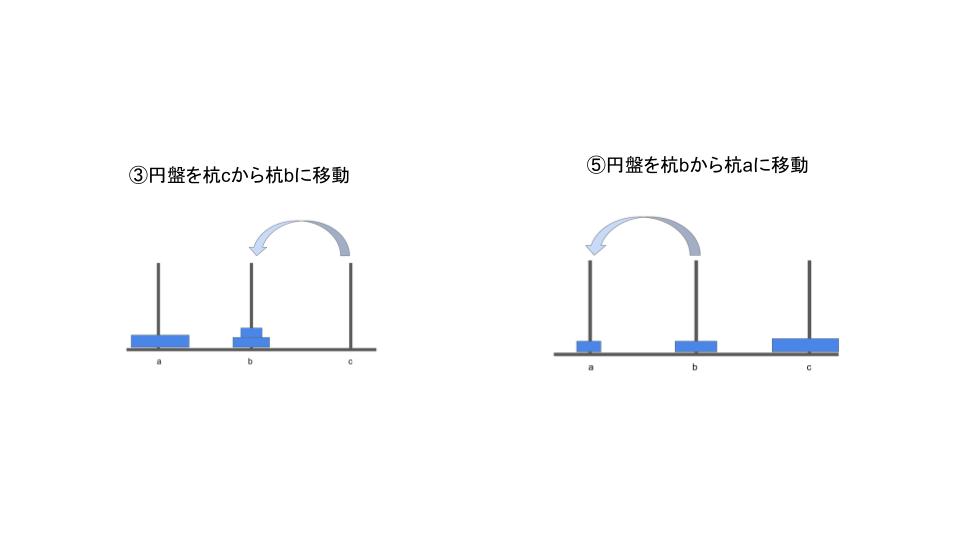
この2つの状態の共通点は、移動すべき一番下の円盤を移動対象の杭cに移動できる状態ということです。
③の状態は初期状態で一番下にあった円盤を杭cに移動できる状態です。
⑤の状態は、③の状態で移動し終わった円盤を無視したときに、一番下の円盤が杭bにあり、それを杭cに移動する行程と変わりません。
そして最後⑥の行程で一番上の円盤を杭cに移動することができます。
つまり、③までのゴールは3枚目の円盤を杭cに移動させることがゴールで、⑤までのゴールは2枚目の円盤を杭cに移動させること、⑥は1枚目の円盤を杭cに移動させることがゴールになります。
加えて気づかなければいけない法則があります。
それは、③と⑤の状態のように移動したい円盤を杭cに移動できる状況は杭a→杭c、杭b→杭c、杭a→杭cと交互に訪れていることです。
ここまでのポイントをまとめると以下になります。
- ゴールの円盤(一番下の円盤)を杭cに移動することを考える
- ③と⑤の状態は杭a→杭c、杭b→杭c交互に訪れる
以上のことがわかれば、ハノイの塔アルゴリズムを再起関数を使って表すことができます。
下記がハノイの塔アルゴリズムを表した実際のコードです。
hanoi(3, 'a', 'c', 'b');
function hanoi($n, $from, $to, $work) {
if ($n > 0) {
//1番目の再起関数
hanoi($n-1, $from, $work, $to);
echo $n .'番目の円盤を' . $from . 'から' .$to. 'に移動する';
echo "\n";
//2番目の再起関数
hanoi($n-1, $work, $to, $from);
}
}上記のプログラムを実行した結果が以下になります。
1番目の円盤をAからCに移動する
2番目の円盤をAからBに移動する
1番目の円盤をCからBに移動する
3番目の円盤をAからCに移動する
1番目の円盤をBからAに移動する
2番目の円盤をBからCに移動する
1番目の円盤をAからCに移動する実行結果に問題はなさそうです。
hanoi関数は、第1引数に円盤の数、第2引数で最初に円盤がある杭、第3引数で最終的な移動先、第4引数は移動したい円盤(ゴールの円盤)以外の円盤の待避場所を表しています。
中を見てみると、再起関数が2つ使われています。
これは、③と⑤の状態のように移動したい円盤を杭cに移動できる状況は杭a→杭c、杭b→杭c、杭a→杭cと交互に訪れている法則を表しています。
最初に出てくる再起関数
//1番目の再起関数
hanoi($n-1, $from, $work, $to);では、一番下の円盤を移動するための事前準備をしています。ここでは、移動前(枚数はn枚とは限らない)に積み上がっている$fromの杭から一番下の円盤(ゴールの円盤)を移動するために一時保管の杭$workに円盤を移動させています。
一番下の円盤を移動させる準備ができたら、下記で移動させます。
echo $n .'番目の円盤を' . $from . 'から' .$to. 'に移動する';その後に出てくる再起関数では、一番下の円盤を移動させるために一時保管の杭$workに移動してあったその他の円盤を移動先の$toの杭に移動させています。
//2番目の再起関数
hanoi($n-1, $work, $to, $from);ハノイの塔アルゴリズムを理解する上で、大切だったのは個々の移動の流れを追うのではなく、流れ全体をみてどのようにコードに落とし込めるかを考えることでした。
そして、上記のコードの流れを理解した上で結局はn=1から流れを追っていことで、どのようにコードが再起関数を解釈しているかを理解することができました。
ハノイの塔アルゴリズムはさまざまなところで解説されていますが、どうしても理解できない場合、n=1からデータの流れを追っていくことで理解できるようになるかもしれません。
 takatoku-room
takatoku-room 
